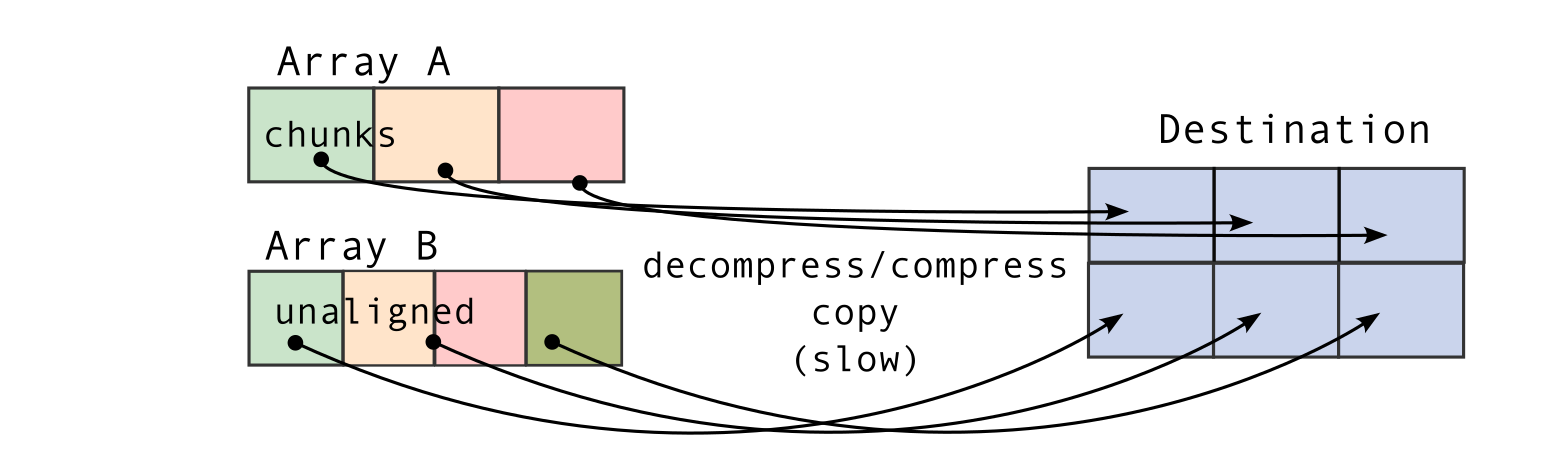
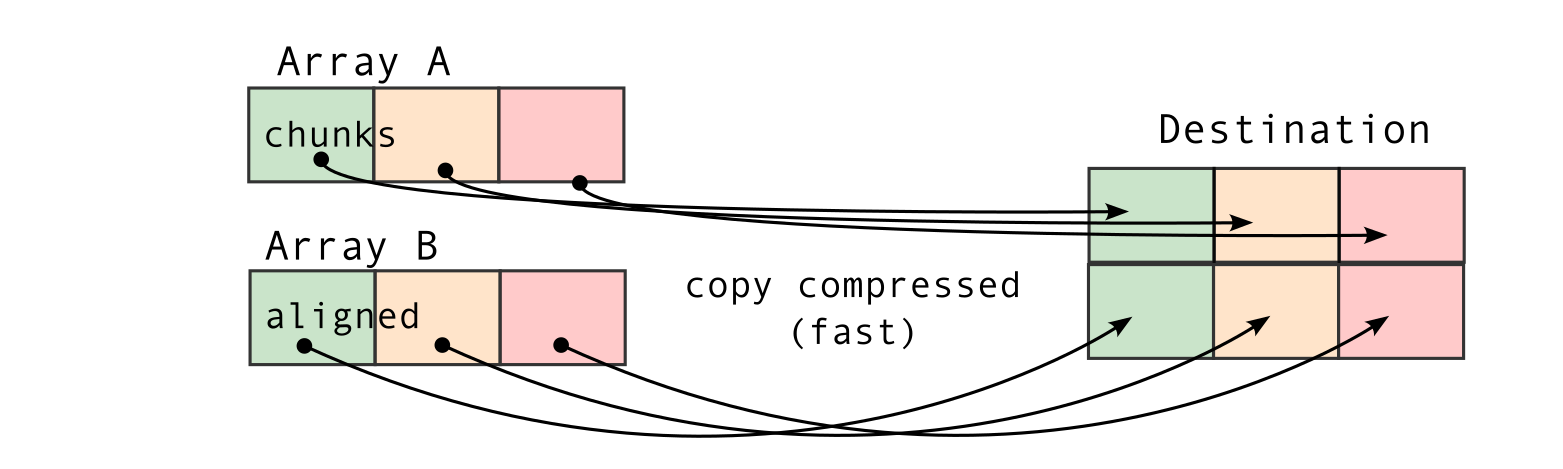
Blosc2 Gets Fancy (Indexing)
In response to requests from our users, the Blosc2 team has introduced a fancy indexing capability into the flagship Blosc2 NDArray object. In the future, this could be extended to other classes within the Blosc2 library, such as C2Array and LazyArray.
What is Fancy Indexing?
In many array libraries, most famously NumPy, fancy indexing refers to a vectorized indexing format which allows for simultaneous selection and reshaping of arrays (see this excerpt). For example, one may wish to select three entries from a 1D array:
arr = array([10, 11, 12])
which can be done like so:
arr[[1,2,1]] >> array([11, 12, 11])
Note that the order of the indices is arbitrary (i.e. the elements of the output may occur in a different order to the original array) and indices may be repeated. Moreover, if the array is multidimensional, for example:
arr = array([[10, 11],
[12, 13],
[14, 15]])
then the output consists of the relevant rows:
arr[[1,2,0]]
>> array([[12, 13],
[14, 15],
[10, 11]])
and so on for arbitrary numbers of dimensions.
Indeed one can output arbitrary shapes, for example via:
arr[[[1,2],[0,1]]]
>> array([[[12, 13],
[14, 15]],
[[10, 11],
[12, 13]]])
NumPy supports many different kinds of fancy indexing, a flavour of which can be seen from the following examples, where row and col are integer array objects. If they are not of the same shape then broadcasting conventions will be applied to try to massage the index into an understandable format.
arr[row]arr[[row, col]]arr[row, col]arr[row[:, None], col]arr[1, col]orarr[1:9, col]
In addition, one may use a boolean mask, in combination with integer indices, slices, or integer arrays via
arr[row[:, None], mask]
where the mask must have the same length as the indexed dimension(s).
Support for Fancy Indexing and ndindex
Other libraries for management of large arrays such as zarr and h5py offer fancy indexing support but neither are as comprehensive as NumPy. h5py, which uses the HDF5 format, is quite limited in that one may only use one integer array, no repeated indices are allowed, and the array must be sorted in increasing order, although mixed slice and integer array indexing is possible.
zarr, via its vindex (for vectorized index), offers more support, but is rather limited when it comes to mixed indexing, as slices may not be used with integer arrays, and an integer array must be provided for every dimension of the array (i.e. arr[row] fails on any non-1D arr).
This makes it difficult (in the case of zarr) or impossible (in the case of h5py) to do the kind of reshaping we saw in the introduction (i.e. case 2 above arr[[[1,2],[0,1]]]). This lack of support is due to a combination of: 1) the computational difficulty of many of these operations; and 2) the at times counter-intuitive behaviour of fancy indexing (see the end of this blog post for more details).
When implementing fancy indexing for Blosc2 we strove to match the functionality of NumPy as closely as possible, and we have almost been able to do so — all the 6 cases mentioned above are perfectly feasible with this new Blosc2 release! There are only some minor edge cases which are not supported (see Example 2 in the Addendum). This would not have been possible without the excellent ndindex library, which offers many very useful, efficient functions for index conversion between different shapes and chunks. We can then call NumPy behind-the-scenes, chunk-by-chunk, and exploit its native support for fancy indexing, without having to load the entire array into memory.
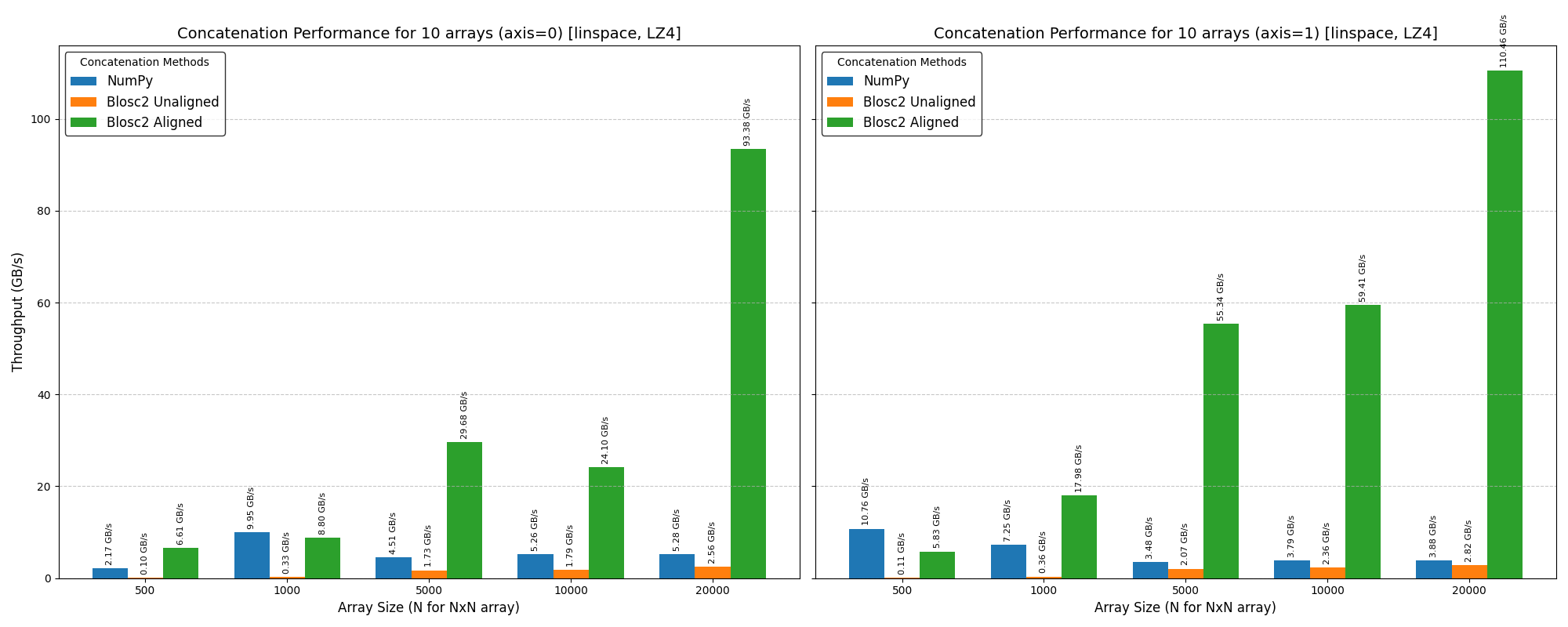
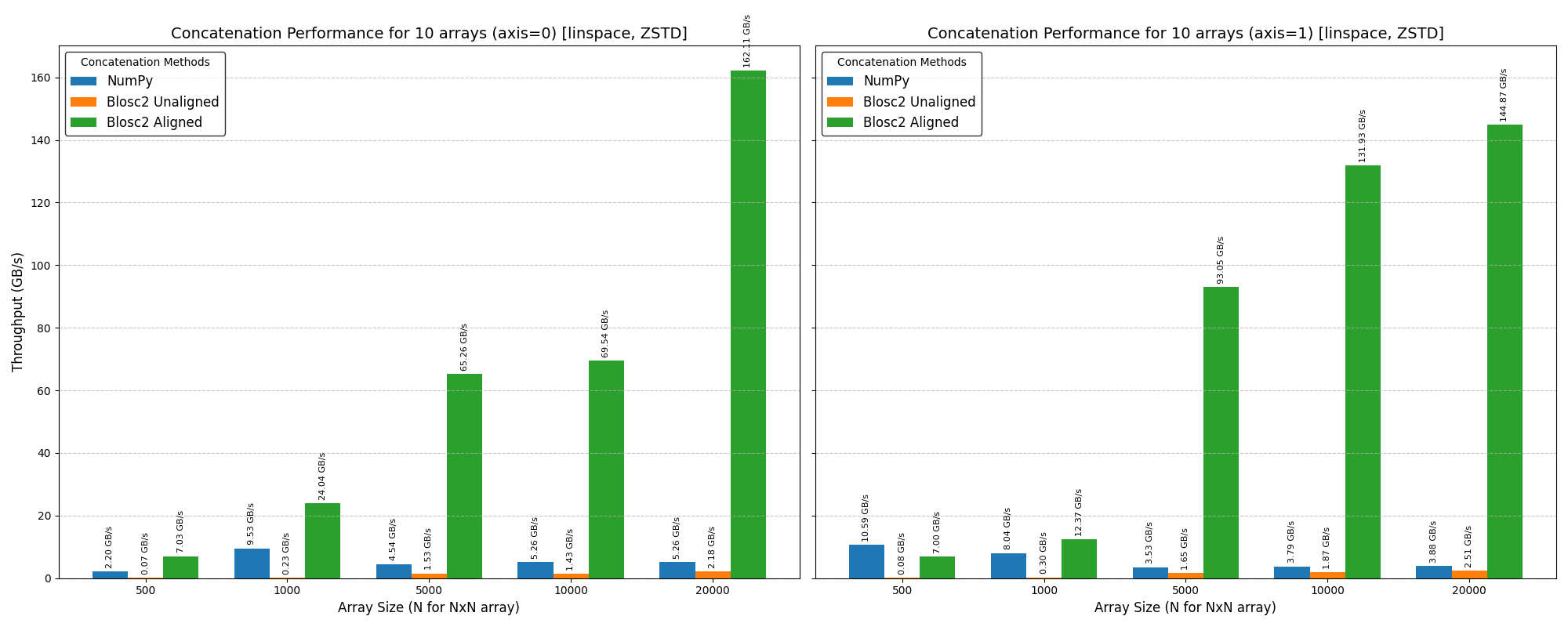
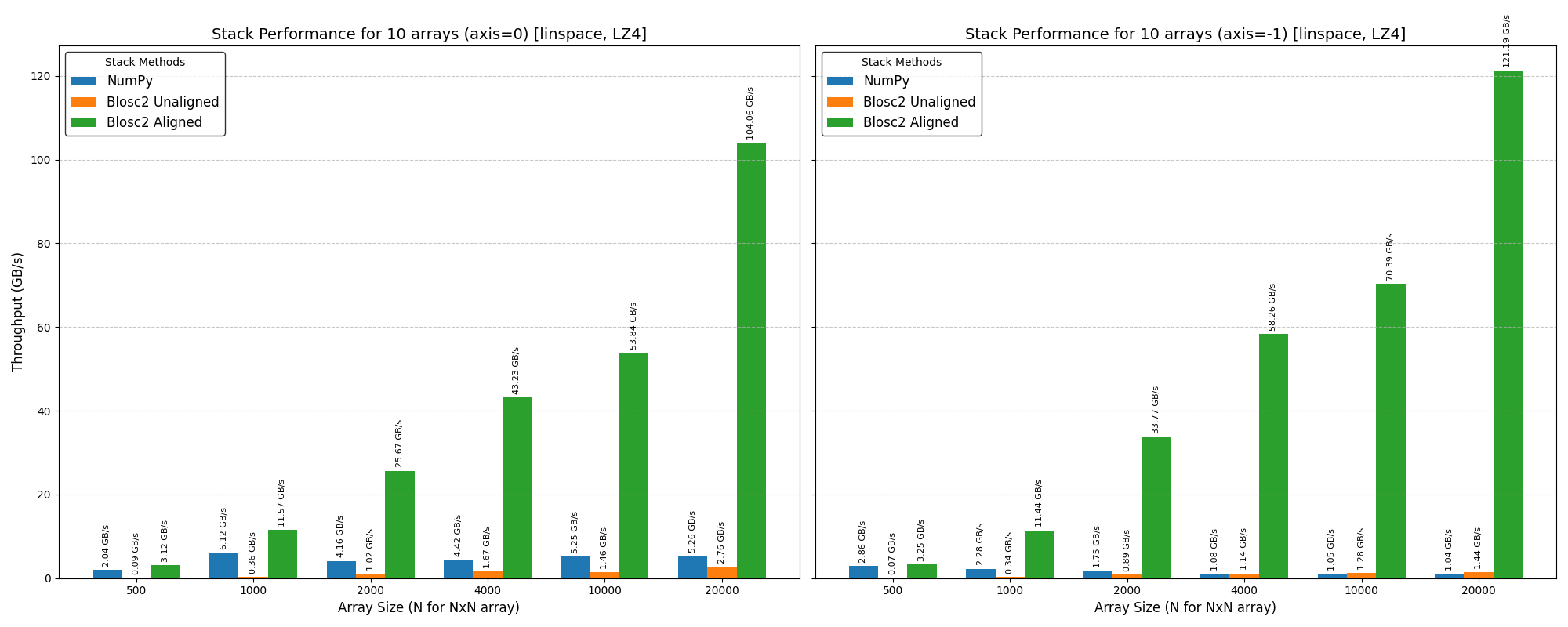
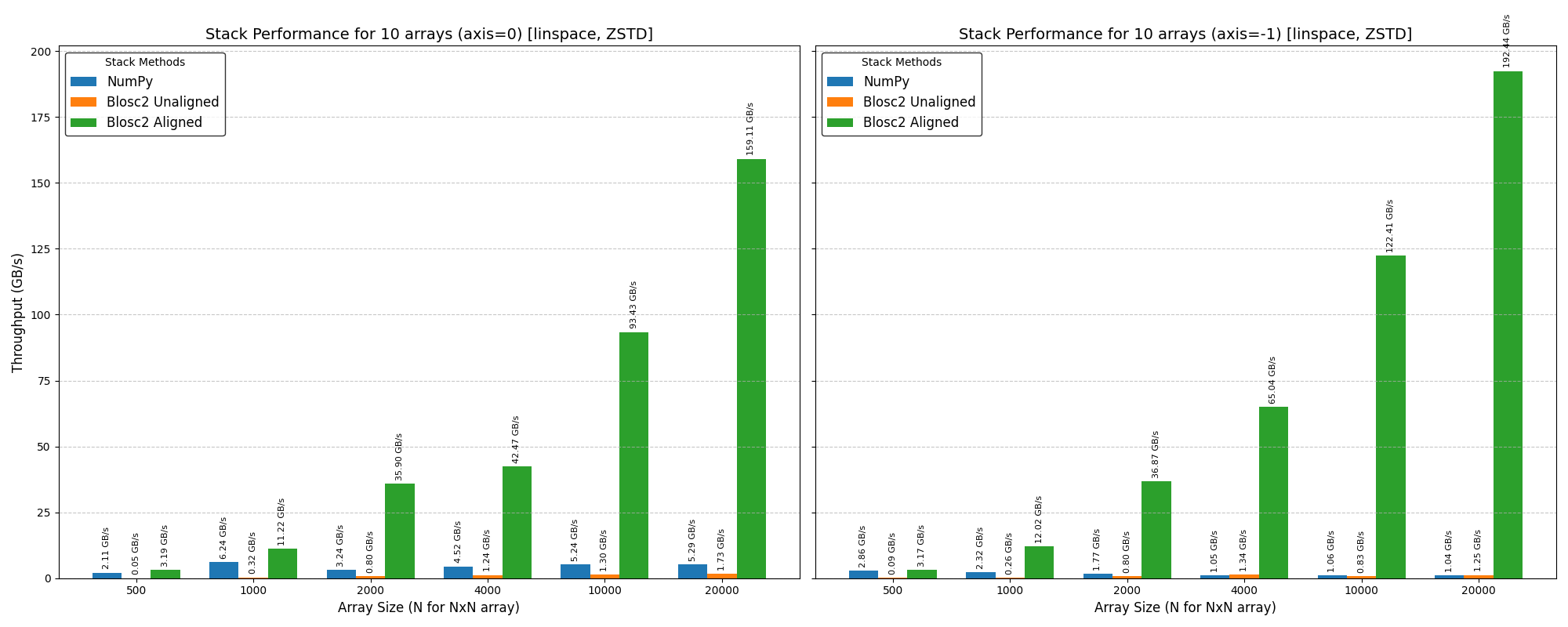
Results: Blosc2, Zarr, H5Py and NumPy
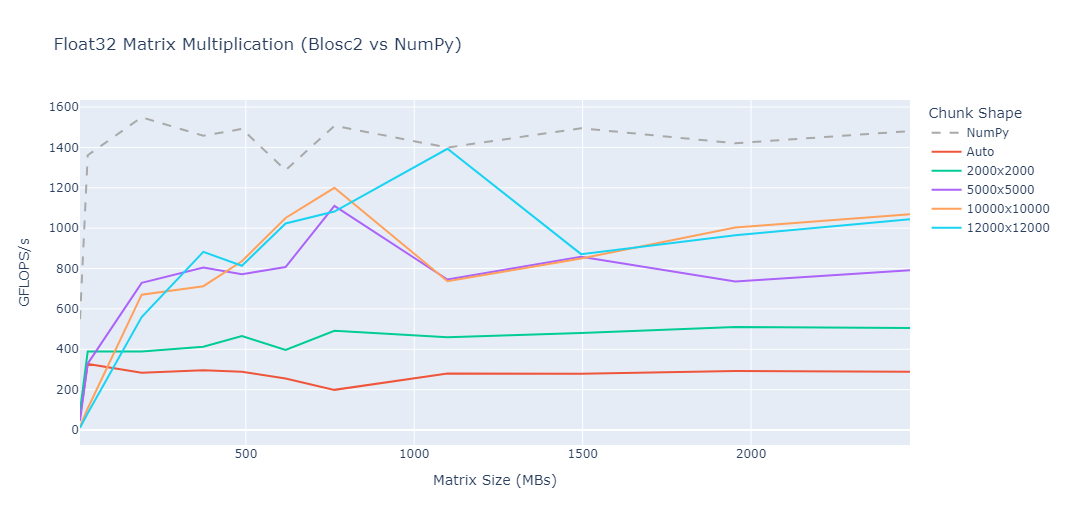
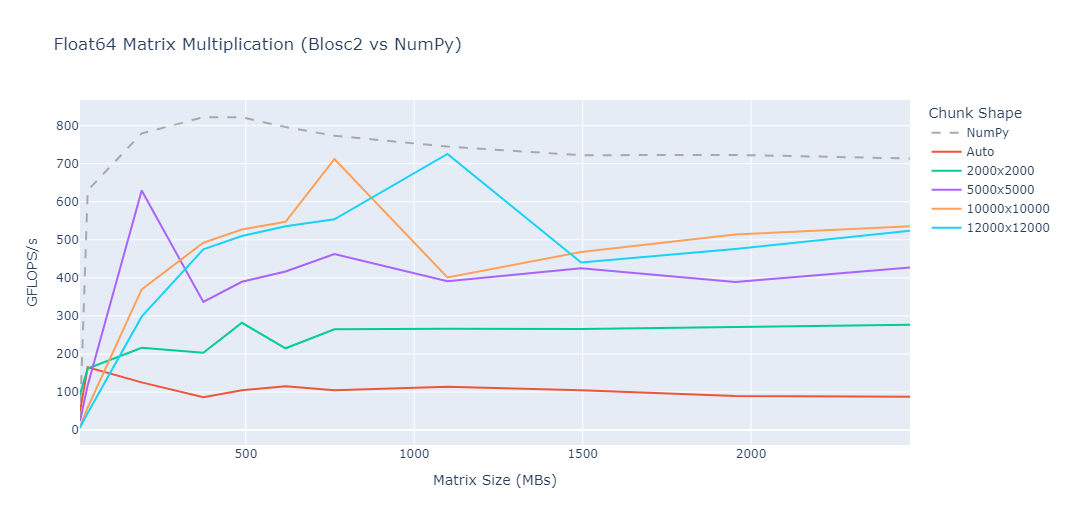
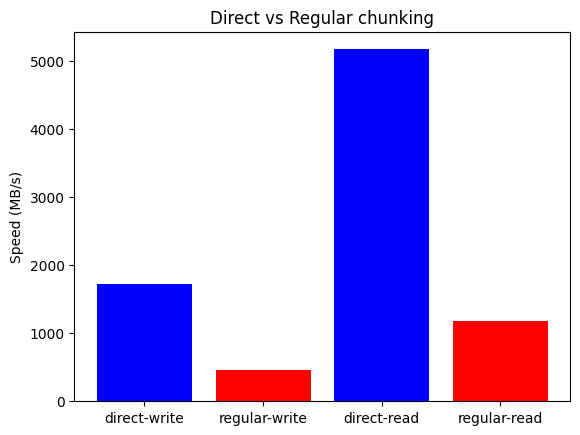
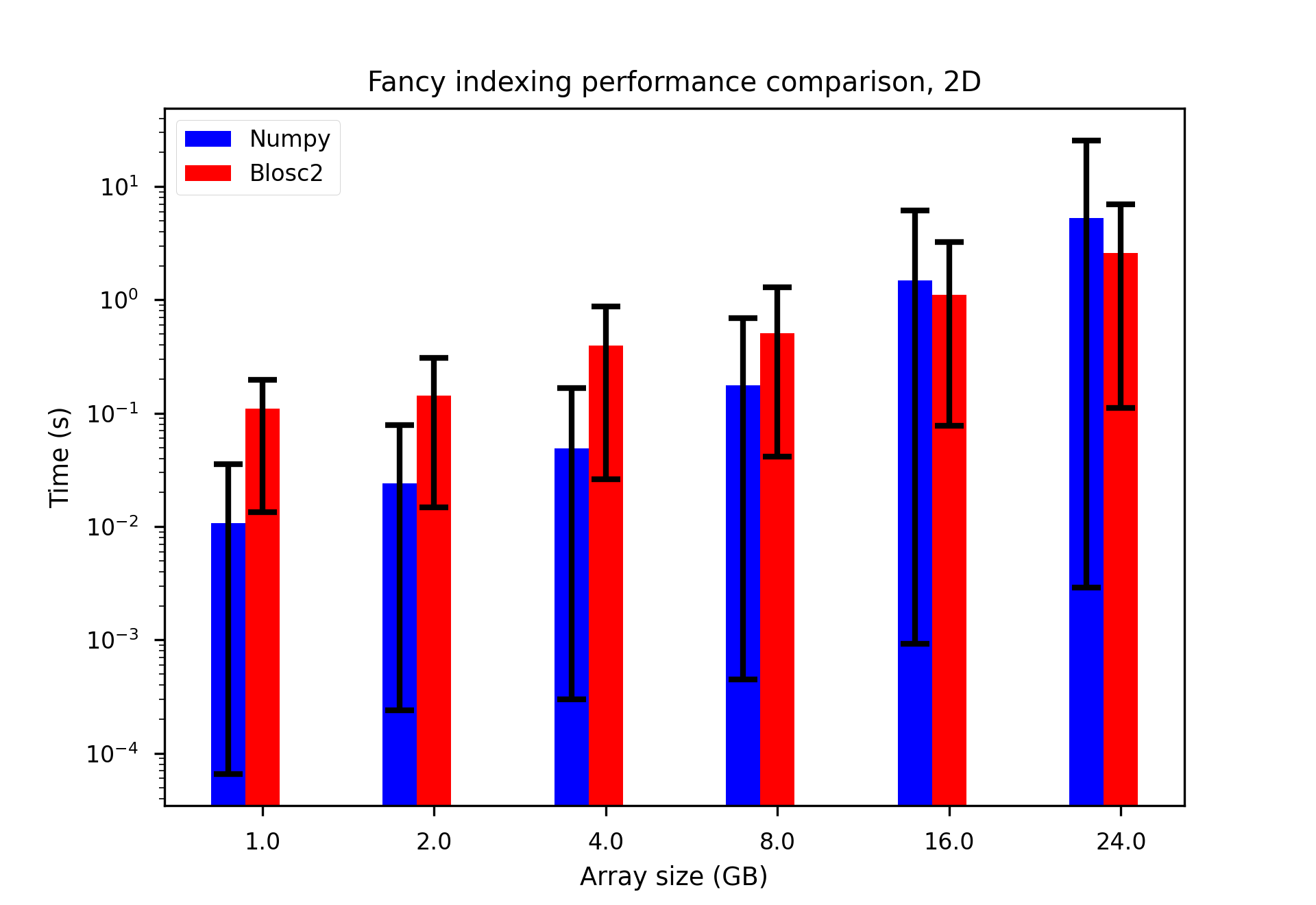
Hence, when averaging over the indexing cases above on 2D arrays of varying sizes, we observe only a minor slowdown for Blosc2 compared to NumPy when the array size is small compared to total memory (24GB), suggesting a small chunking-and-indexing overhead. As expected, when the array grows to an appreciable fraction of memory (16GB), loading the full NumPy array into memory starts to impact performance. The black error bars in the plots indicate the maximum and minimum times observed over the indexing cases (for which there is clearly a large variation).
Note that for cases 4 and 6 with large row or col index arrays, broadcasting causes the resulting index (stored in memory) to be very large, and even for array sizes of 2GB computation is too slow. In the future, we would like to see if this can be improved.
Blosc2 is also as fast or faster than Zarr and HDF5 even for the limited use cases that the latter two libraries both support. HDF5 in particular is especially slow when the indexing array is very large.
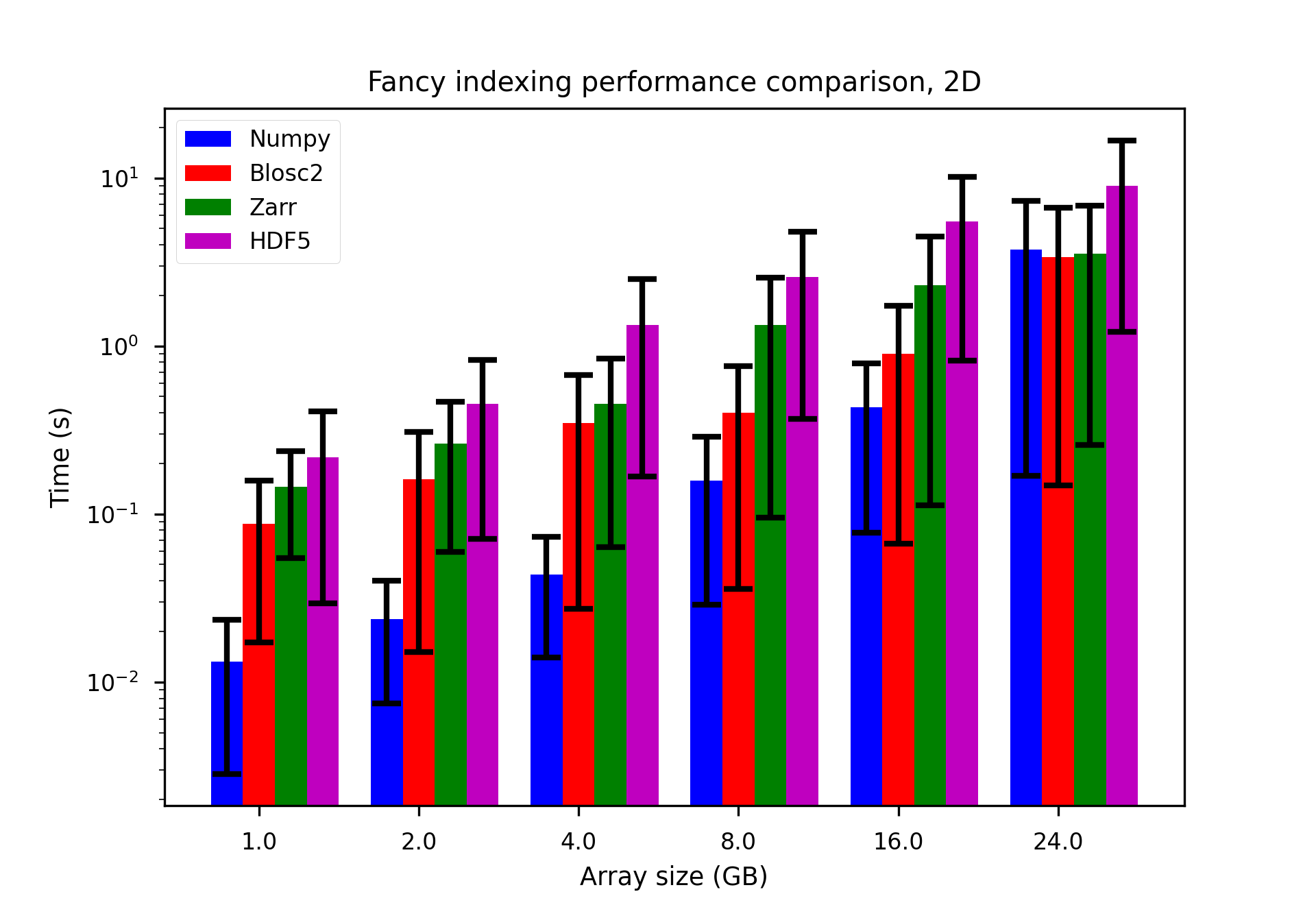
These plots have been generated using a Mac mini with the Apple M4 Pro processor. The benchmark is available on the Blosc2 github repo here.
Conclusion
Blosc2 offers a powerful and flexible fancy indexing functionality that is more extensive than that of Zarr and H5Py, while also being able to handle large arrays on-disk without loading them into memory. This makes it a great choice for applications that require complex indexing operations on large datasets. Give it a try in your own projects! If you have questions, the Blosc2 community is here to help.
If you appreciate what we're doing with Blosc2, please think about supporting us. Your help lets us keep making these tools better.
Addendum: Oindex, Vindex and FancyIndex via Two Examples
Zarr's implementation of fancy indexing is packaged as vindex (vectorized indexing). It also offers another indexing functionality, called orthogonal indexing, via oindex.
The reason for this dual support becomes clear when one considers a simple example.
Example 1
For a 2D array, we have seen that the fancy-indexing rules will cause the two index arrays below to be broadcast together:
arr[[0, 1], [2, 3]] -> [arr[0,2], arr[1,3]]
giving an output with two elements of shape (2,). This is vindexing.
However, one could understand this indexing as selecting rows 0 and 1 in the array, and then their intersection with columns 2 and 3. This gives an output with four elements of shape (2, 2), with elements:
[[arr[0,2], arr[0,3]], [arr[1,2], arr[1,3]]]
This is oindexing. Clearly, given the same index, the output is in general different; it is for this reason that the debate about fancy indexing can be quite polemical, and why there is a movement to introduce the vindex/oindex duality in NumPy.
Example 2
I have glossed over this until now, but vindex is not the same as fancy indexing. For this reason Zarr does not support all the functionality of fancy indexing, since it only supports vindex. The most important distinction between the two is that it seeks to avoid certain unexpected fancy indexing behaviour, as can be seen by considering a 3D NumPy array of shape (X, Y, Z) as in the example here. Consider the unexpected behaviour of:
arr[:10, :, [0,1]] has shape (10, Y, 2). arr[0, :, [0, 1]] has shape (2, Y), not (Y, 2)!!
NumPy indexing treats non-slice indices differently, and will always put the axes introduced by the index array first, unless the non-slice indexes are consecutive, in which case it will try to massage the result to something intuitive (which normally coincides with the result of an oindex) — hence arr[:, 0, [0, 1]] has shape (X, 2), not (2, X).
The hypothesised NumPy vindex would eliminate this transposition behaviour, and be internally consistent, always putting the axes introduced by the index array first. Unfortunately, this is difficult and costly, and so the alternative is to simply not allow such indexing and throw an error, or force the user to be very specific.
Blosc2 will throw an error when one inserts a slice between array indices:
arr[:, 0, [0, 1]] -> shape (X, 2) arr.vindex[0, :, [0,1]] -> ERROR
Zarr's vindex (called by __getitem__), by requiring integer array indices for all dimensions, throws an error for all mixed indices of this type:
arr[:, 0, [0, 1]] -> ERROR arr[0, :, [0,1]] -> ERROR
Thus to reproduce the result of Blosc2 for the first case, one must use an explicit index array:
idx = np.array([0,1]).reshape(1,-1) arr[np.arange(X).reshape(-1,1), 0 , idx] -> shape (X, 2)
For both Blosc2 and Zarr, one must use an explicit index array like so for the second case:
arr[0, np.arange(Y).reshape(-1,1), idx] -> shape (Y, 2)
Hopefully you now understand why fancy indexing can be so tricky, and why few libraries seek to support it to the same extent as NumPy - some would say it is perhaps not even desirable to do so!